Decoding The Pupil’s T-Desk: A Complete Information

Decoding the Pupil’s t-Desk: A Complete Information

Associated Articles: Decoding the Pupil’s t-Desk: A Complete Information

Introduction

On this auspicious event, we’re delighted to delve into the intriguing subject associated to Decoding the Pupil’s t-Desk: A Complete Information. Let’s weave attention-grabbing info and provide contemporary views to the readers.

Decoding the Pupil’s t-Desk: A Complete Information

The Pupil’s t-distribution, a cornerstone of statistical inference, performs an important function in speculation testing and confidence interval estimation when coping with small pattern sizes or unknown inhabitants commonplace deviations. In contrast to the conventional distribution, the t-distribution’s form varies relying on the levels of freedom (df), a parameter reflecting the pattern dimension. Understanding the Pupil’s t-table, an important software for accessing essential t-values, is crucial for accurately decoding statistical outcomes. This text supplies an in depth clarification of the t-table, its development, interpretation, and sensible purposes.

Understanding the t-Distribution:

The t-distribution, developed by William Sealy Gosset below the pseudonym "Pupil," arises from the ratio of a usually distributed random variable to an impartial chi-squared random variable divided by its levels of freedom. This seemingly complicated definition interprets to a sensible implication: when coping with small samples (sometimes lower than 30 observations), the t-distribution supplies a extra correct illustration of the sampling distribution of the imply than the conventional distribution. Because the pattern dimension will increase, the t-distribution progressively approaches the conventional distribution.

The important thing parameter figuring out the form of the t-distribution is the levels of freedom (df). For a single-sample t-test, the levels of freedom are calculated as:

df = n - 1

the place ‘n’ is the pattern dimension. For extra complicated analyses, corresponding to impartial samples t-tests or ANOVA, the calculation of levels of freedom turns into extra intricate, however the basic precept stays the identical – it displays the variety of impartial items of data accessible to estimate the inhabitants variance.

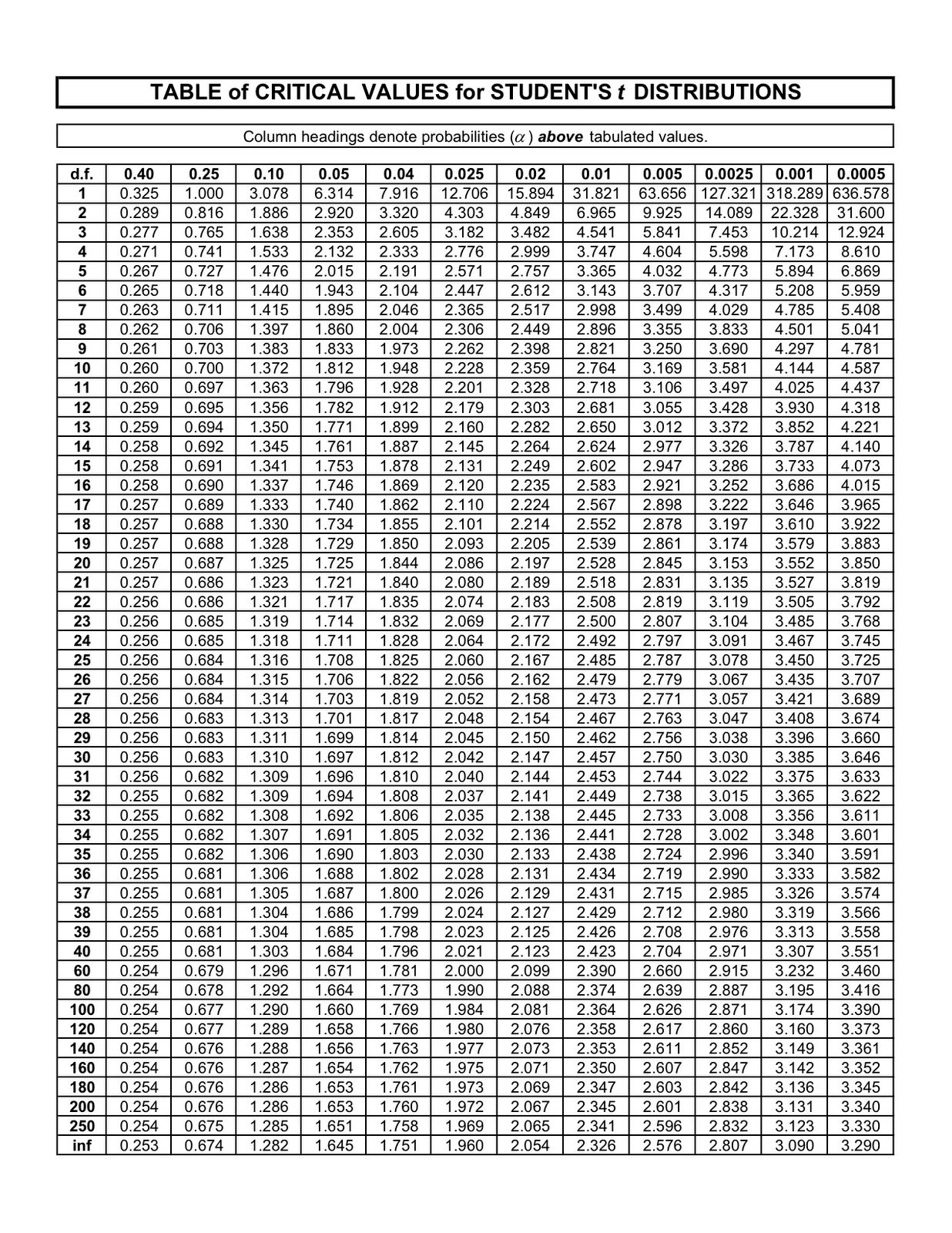
The Construction of the Pupil’s t-Desk:

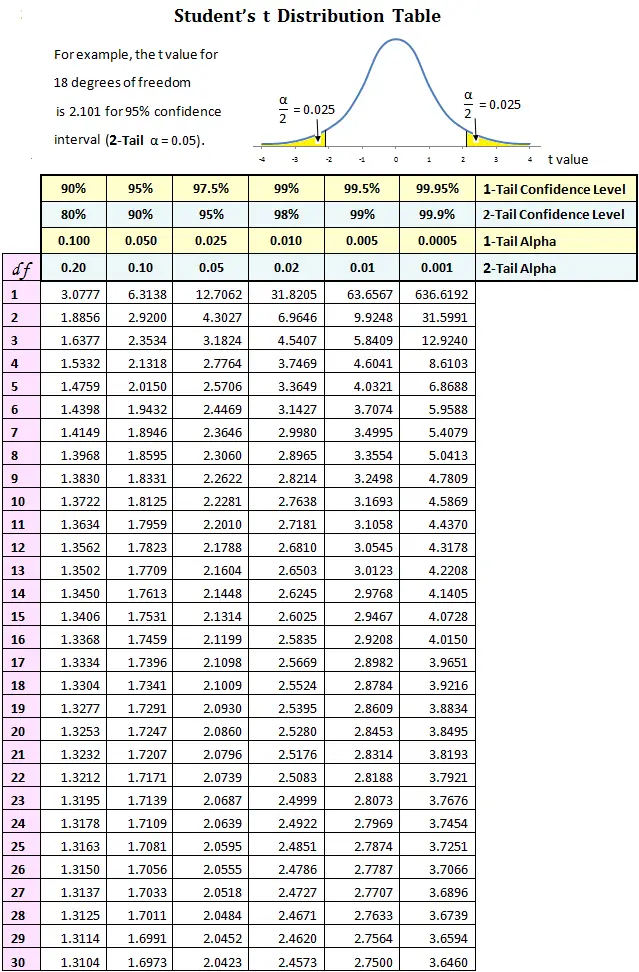
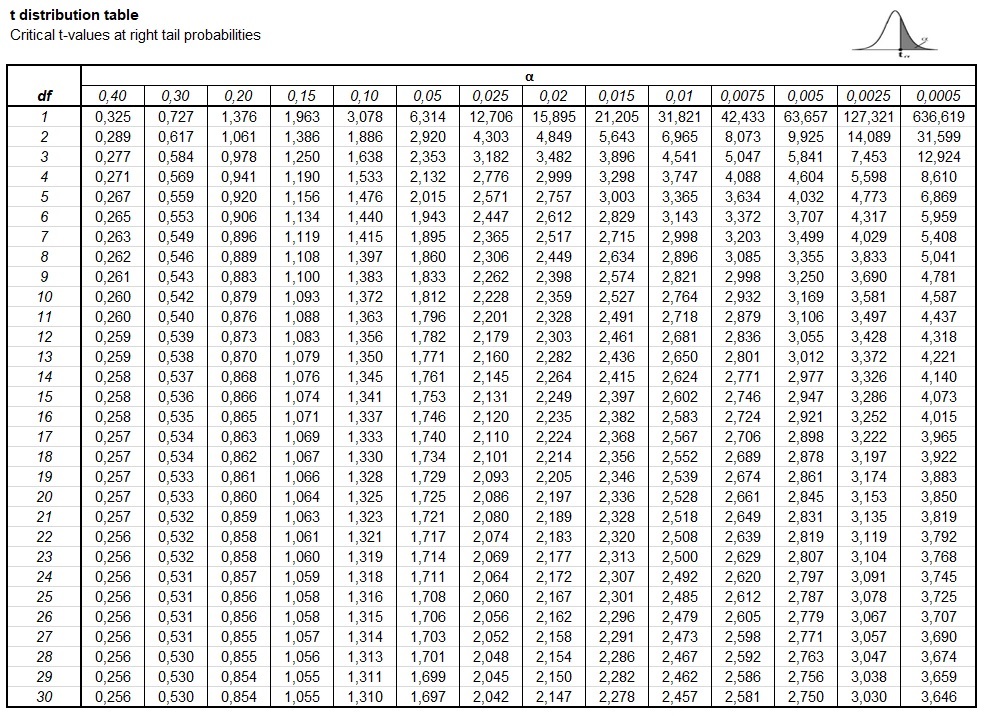
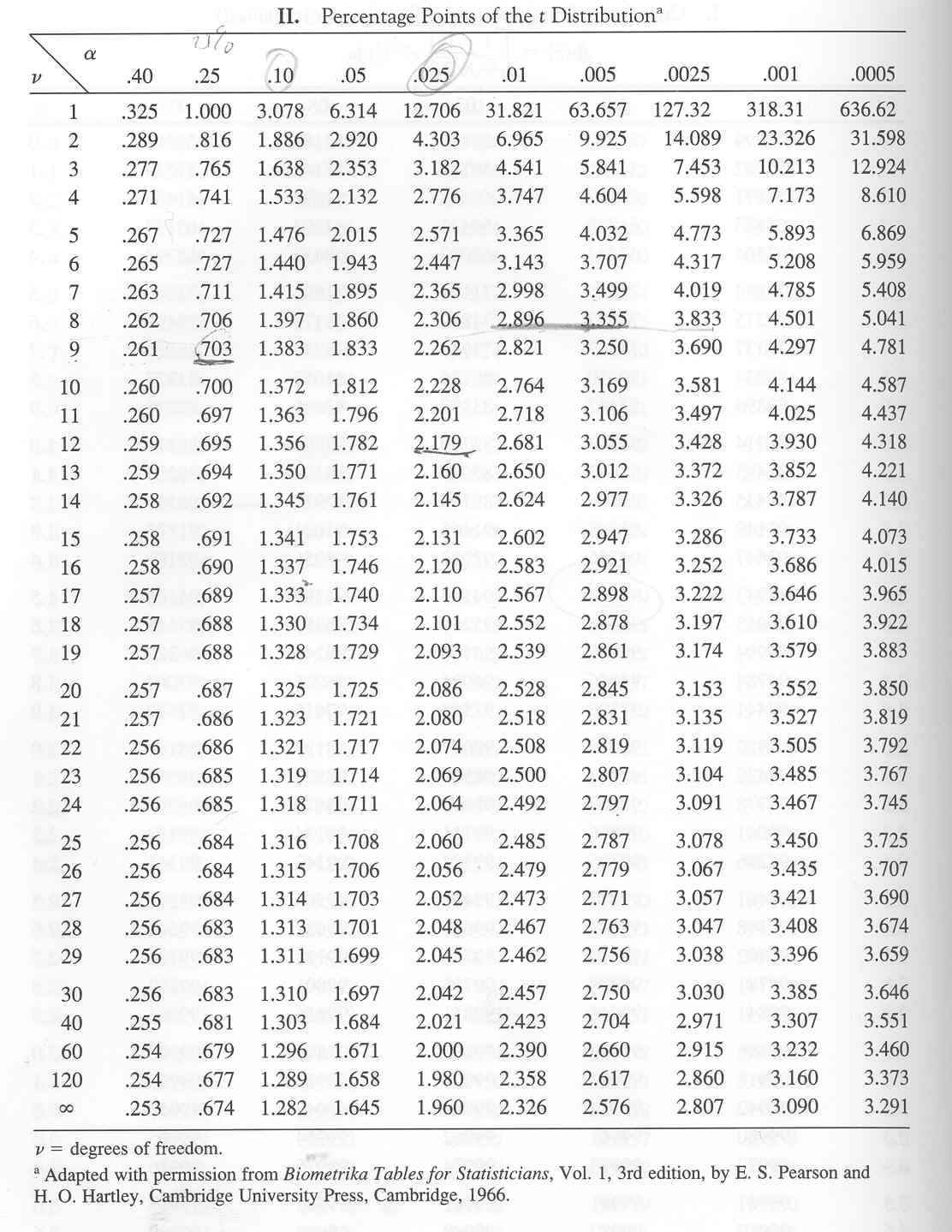
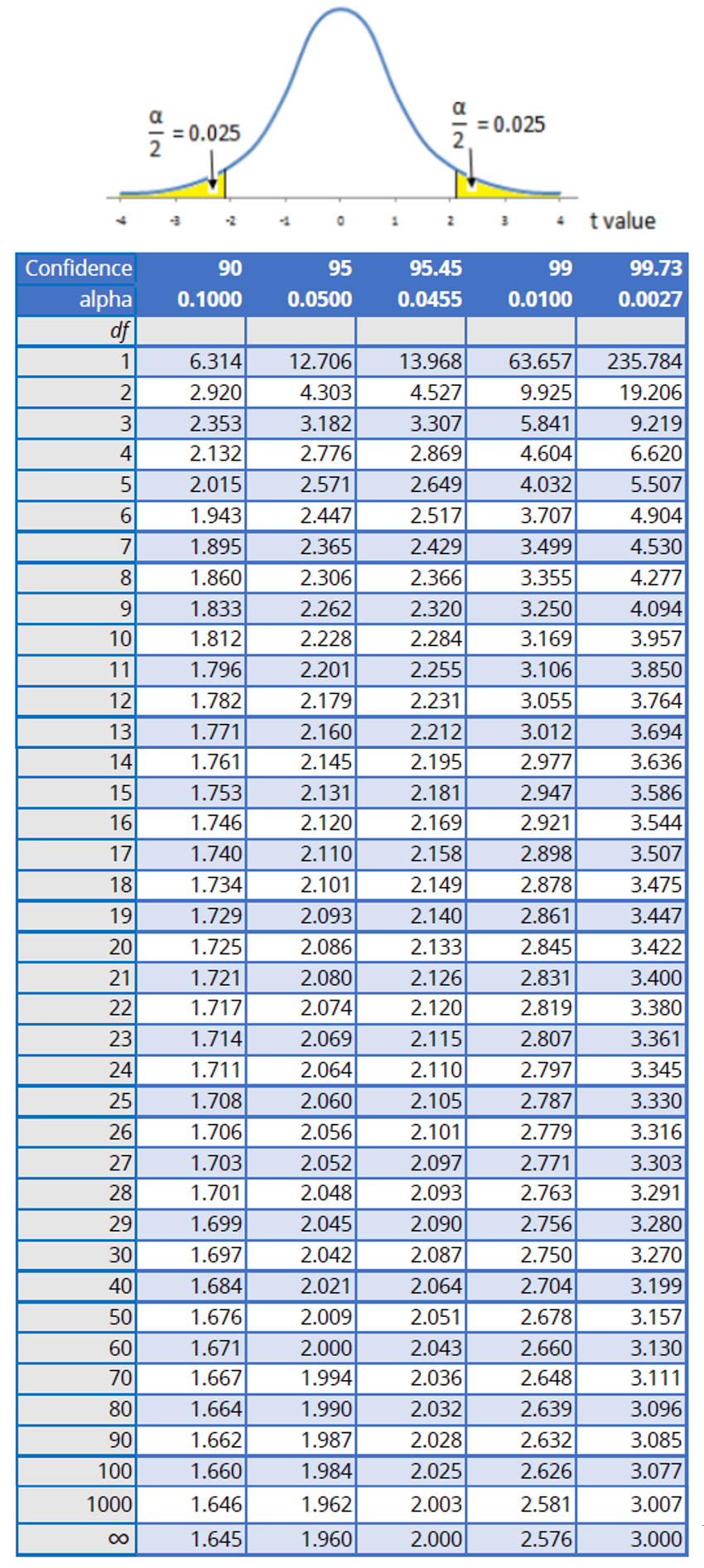
A typical Pupil’s t-table is organized as a matrix. The rows symbolize the levels of freedom (df), starting from 1 to infinity (typically approximated by a big worth like 100 or 120). The columns symbolize the chance (or significance degree, typically denoted as α) related to a given essential t-value. Frequent significance ranges embrace 0.10, 0.05, 0.025, 0.01, and 0.005, representing one-tailed exams. For 2-tailed exams, these values are doubled (e.g., 0.05 turns into 0.10).

Deciphering the t-Desk:

To make use of the t-table successfully, you might want to know:

1. Levels of Freedom (df): That is decided by your pattern dimension and the kind of t-test being carried out.

2. Significance Stage (α): This represents the chance of rejecting the null speculation when it’s really true (Sort I error). The selection of α relies on the context of the research and the researcher’s danger tolerance. A typical alternative is α = 0.05.

3. One-tailed or Two-tailed Check: A one-tailed take a look at examines the impact in just one route (e.g., whether or not the imply is larger than a particular worth), whereas a two-tailed take a look at examines the impact in each instructions (e.g., whether or not the imply is totally different from a particular worth).

Upon getting these three items of data, you find the corresponding row (df) and column (α) within the t-table. The worth on the intersection is the essential t-value. This essential t-value serves as a threshold: in case your calculated t-statistic (obtained out of your information evaluation) exceeds the essential t-value (in absolute worth for two-tailed exams), you reject the null speculation.

Instance:

As an instance you performed a one-sample t-test with a pattern dimension of 15 (df = 14) and a significance degree of α = 0.05 for a one-tailed take a look at. Trying up df = 14 and α = 0.05 within the t-table, you discover a essential t-value of roughly 1.761. In case your calculated t-statistic is larger than 1.761, you’ll reject the null speculation on the 0.05 significance degree. If it had been a two-tailed take a look at, you’d search for the essential t-value at α = 0.10 (doubled significance degree) which might be roughly 1.761.

Purposes of the t-Desk:

The t-table is an important software in varied statistical purposes:

• One-sample t-test: Evaluating the imply of a single pattern to a identified inhabitants imply.

• Unbiased samples t-test: Evaluating the technique of two impartial teams.

• Paired samples t-test: Evaluating the technique of two associated teams (e.g., earlier than and after measurements on the identical topics).

• Confidence interval estimation: Setting up confidence intervals for inhabitants means. The t-table supplies the essential t-value used to calculate the margin of error.

• Regression evaluation: Assessing the importance of regression coefficients.

Limitations and Concerns:

Whereas the t-table is a robust software, it has limitations:

• Assumption of normality: The t-test assumes that the information are roughly usually distributed. Extreme deviations from normality can have an effect on the validity of the outcomes. Non-parametric alternate options must be thought-about if normality is violated.

• Equal variances (for impartial samples t-test): The impartial samples t-test assumes equal variances within the two teams. If this assumption is violated, a modified t-test (e.g., Welch’s t-test) must be used.

• Pattern dimension: The accuracy of the t-test will increase with bigger pattern sizes. For very small pattern sizes, the t-distribution might not precisely mirror the sampling distribution.

Technological Developments and Options:

Whereas t-tables stay worthwhile for understanding the underlying ideas of speculation testing, statistical software program packages (like R, SPSS, SAS, and Python with libraries like SciPy) readily calculate p-values and demanding t-values, eliminating the necessity for handbook desk lookup. These packages additionally provide extra sturdy exams that handle violations of assumptions related to the standard t-test.

Conclusion:

The Pupil’s t-table is an indispensable software for conducting speculation exams and setting up confidence intervals when coping with small pattern sizes or unknown inhabitants variances. Understanding its construction, interpretation, and limitations is essential for accurately analyzing information and drawing legitimate statistical conclusions. Whereas technological developments have simplified the method of acquiring essential t-values, mastering using the t-table supplies a basic understanding of the t-distribution and its function in statistical inference. It is a worthwhile talent for any aspiring statistician or researcher. Bear in mind at all times to think about the assumptions underlying the t-test and select the suitable statistical technique primarily based on the traits of your information.

Closure

Thus, we hope this text has offered worthwhile insights into Decoding the Pupil’s t-Desk: A Complete Information. We thanks for taking the time to learn this text. See you in our subsequent article!