Decoding The Z-Chart: A Complete Information To Commonplace Regular Distribution

Decoding the Z-Chart: A Complete Information to Commonplace Regular Distribution

Associated Articles: Decoding the Z-Chart: A Complete Information to Commonplace Regular Distribution

Introduction

With enthusiasm, let’s navigate by means of the intriguing subject associated to Decoding the Z-Chart: A Complete Information to Commonplace Regular Distribution. Let’s weave attention-grabbing data and provide contemporary views to the readers.

Decoding the Z-Chart: A Complete Information to Commonplace Regular Distribution

The Z-chart, also called the usual regular distribution desk, is a cornerstone of statistical evaluation. It is a essential instrument for understanding chances related to usually distributed information, enabling us to make inferences and draw conclusions about populations primarily based on pattern information. This complete information will delve into the intricacies of the Z-chart, exploring its development, purposes, and limitations, empowering you to confidently make the most of this highly effective statistical instrument.

Understanding the Commonplace Regular Distribution

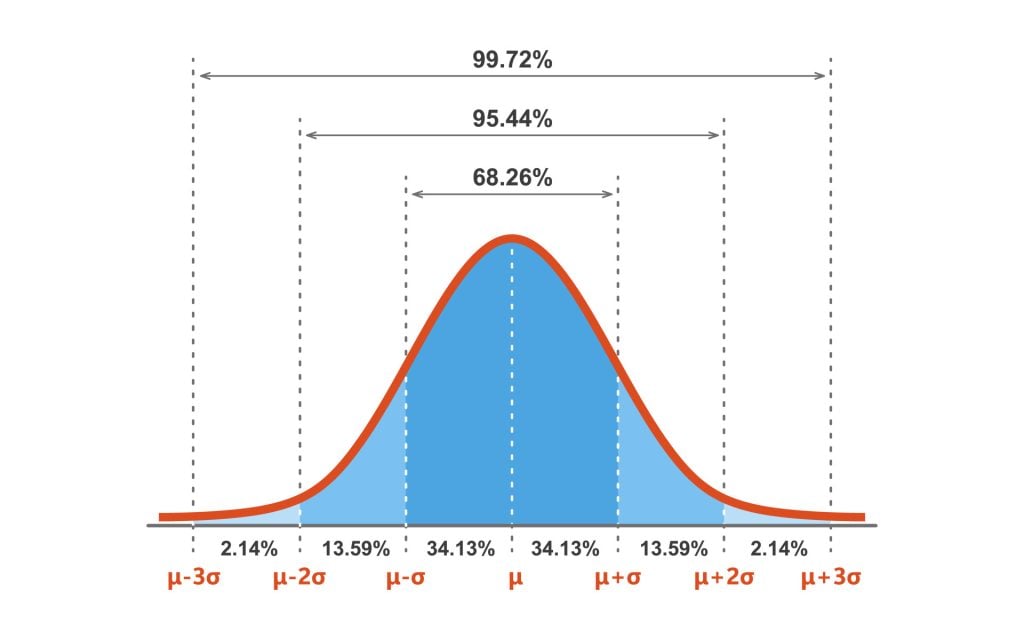
Earlier than delving into the mechanics of the Z-chart, it is important to know the idea of the usual regular distribution. A traditional distribution, typically depicted by its attribute bell curve, is a chance distribution that is symmetric round its imply. Many pure phenomena, from human top and weight to check scores and manufacturing defects, approximate a traditional distribution. Nevertheless, totally different regular distributions can have various means and commonplace deviations, making direct comparisons difficult.

The usual regular distribution solves this drawback by standardizing any regular distribution. It has a imply (µ) of 0 and a typical deviation (σ) of 1. This standardization is achieved by means of the Z-score, an important idea linked on to the Z-chart.

The Z-Rating: Remodeling Information into Commonplace Items

The Z-score, also known as the usual rating, represents the variety of commonplace deviations an information level lies from the imply of its distribution. It is calculated utilizing the next formulation:

Z = (X – µ) / σ

The place:

• Z is the Z-score
• X is the person information level
• µ is the inhabitants imply
• σ is the inhabitants commonplace deviation

A optimistic Z-score signifies the information level lies above the imply, whereas a destructive Z-score signifies it lies beneath the imply. A Z-score of 0 means the information level is the same as the imply. As an illustration, a Z-score of 1.5 signifies that the information level is 1.5 commonplace deviations above the imply.

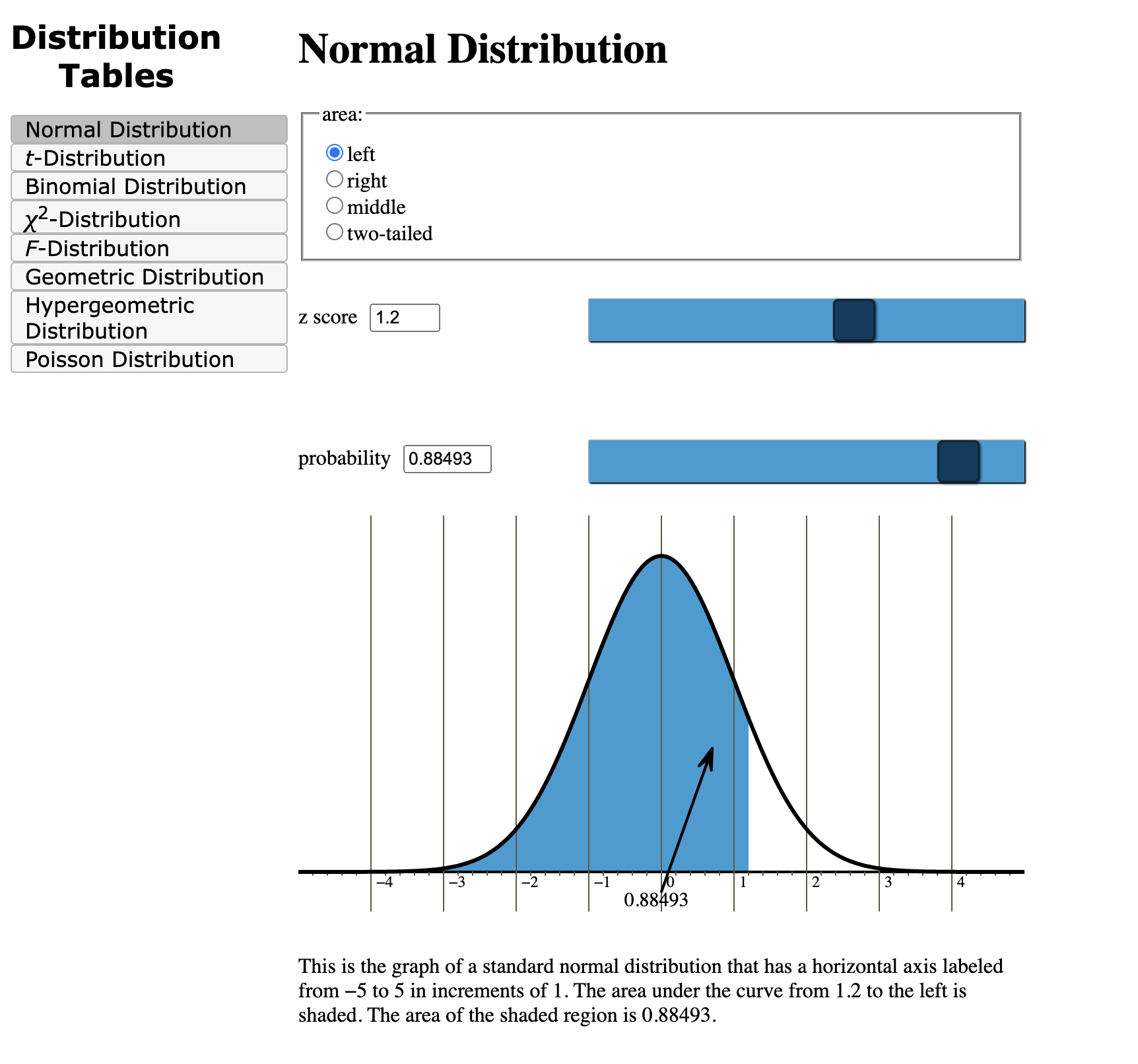
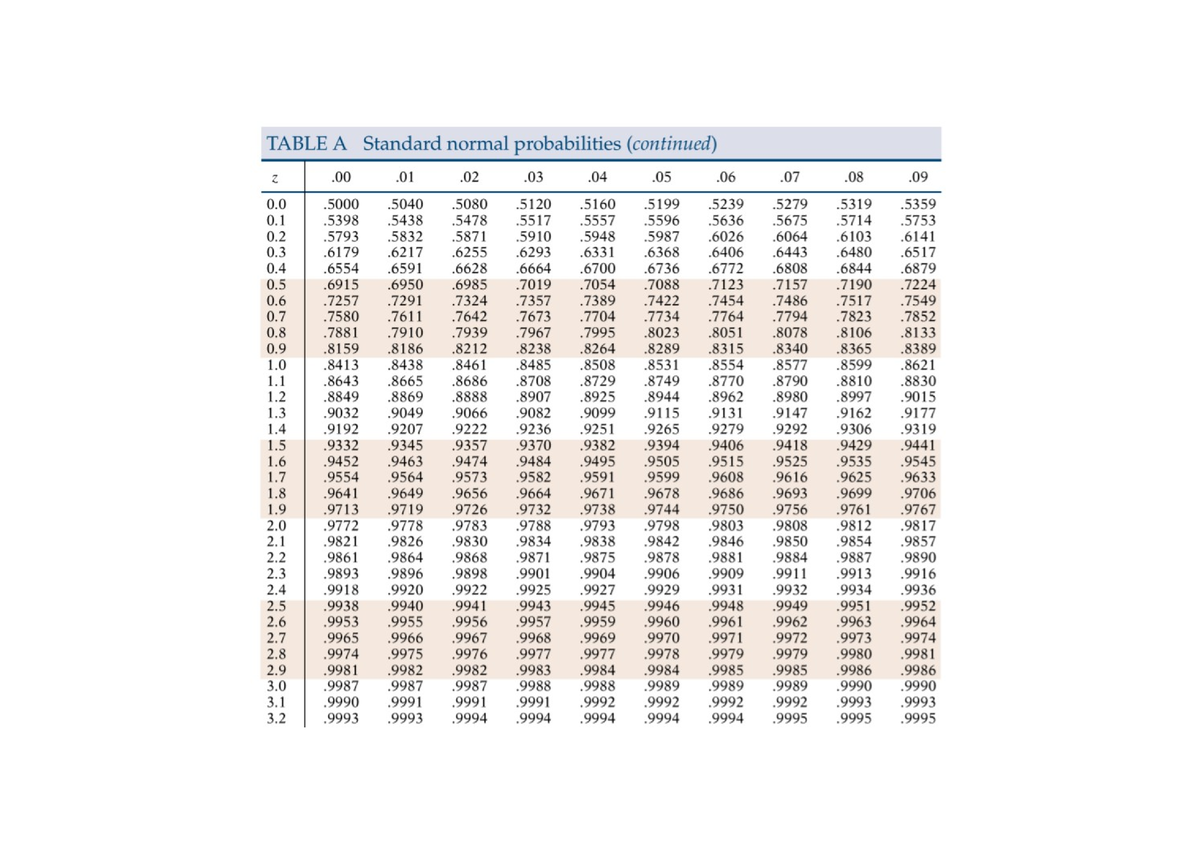
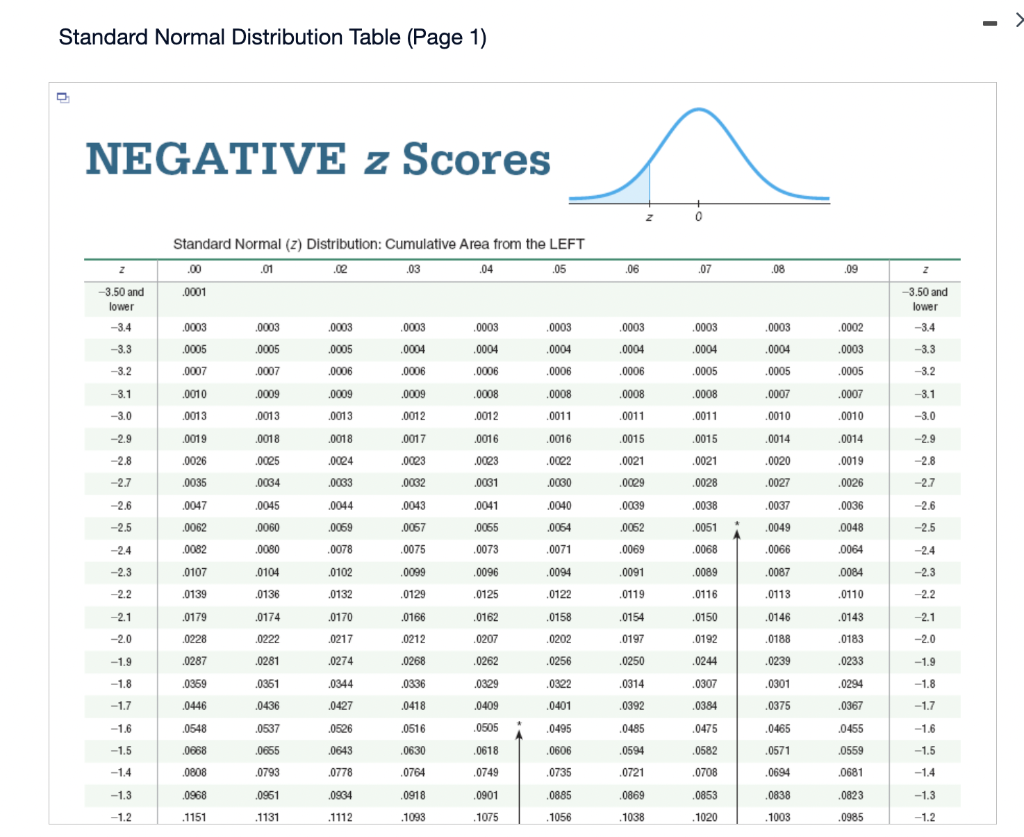
The Z-Chart: A Desk of Chances

The Z-chart is a desk that gives the cumulative chance related to a given Z-score. In different phrases, it tells us the chance of observing a price lower than or equal to a selected Z-score in a typical regular distribution. The desk sometimes shows Z-scores starting from -3.49 to three.49, encompassing nearly the whole chance mass of the usual regular distribution.

The Z-chart is often organized in two elements:

• The Z-score itself: The desk’s rows and columns symbolize the entire and decimal elements of the Z-score respectively. For instance, to seek out the chance related to a Z-score of 1.96, you’d find 1.9 within the rows and 0.06 within the columns.

• The Cumulative Chance: The intersection of the row and column equivalent to the Z-score offers the cumulative chance. This chance represents the world beneath the usual regular curve to the left of the required Z-score. For our instance (Z = 1.96), the cumulative chance is roughly 0.975. This implies there is a 97.5% likelihood of observing a price lower than or equal to 1.96 commonplace deviations above the imply.

Purposes of the Z-Chart

The Z-chart’s versatility makes it an indispensable instrument in varied statistical purposes:

• Speculation Testing: The Z-chart is essential in conducting Z-tests, used to check hypotheses about inhabitants means when the inhabitants commonplace deviation is thought. By calculating the Z-statistic for a pattern imply and evaluating its related chance to a significance degree (e.g., 0.05), we are able to decide whether or not to reject or fail to reject the null speculation.

• Confidence Intervals: The Z-chart performs an important position in developing confidence intervals, which give a variety of values prone to comprise the true inhabitants parameter. As an illustration, a 95% confidence interval for a inhabitants imply makes use of the Z-score equivalent to a cumulative chance of 0.975 (or 2.5% in every tail), sometimes 1.96.

• Chance Calculations: The Z-chart permits us to calculate the chance of observing a price inside a selected vary. As an illustration, to seek out the chance of a price falling between two Z-scores, we merely subtract the cumulative chance of the decrease Z-score from the cumulative chance of the upper Z-score.

• Percentile Calculations: The Z-chart allows us to find out percentiles of a traditional distribution. For instance, to seek out the ninetieth percentile, we glance up the Z-score equivalent to a cumulative chance of 0.90.

• High quality Management: In manufacturing and different industries, the Z-chart is used to observe course of variability and establish outliers. By monitoring Z-scores of course of measurements, we are able to detect deviations from anticipated values and take corrective actions.

Limitations of the Z-Chart

Whereas the Z-chart is a strong instrument, it is important to acknowledge its limitations:

• Assumption of Normality: The Z-chart depends on the idea that the information follows a traditional distribution. If the information is considerably non-normal, utilizing the Z-chart can result in inaccurate outcomes. Assessments for normality, such because the Shapiro-Wilk check, must be performed earlier than making use of the Z-chart.

• Inhabitants Commonplace Deviation: The Z-score calculation requires figuring out the inhabitants commonplace deviation. In lots of real-world situations, the inhabitants commonplace deviation is unknown, necessitating using the t-distribution and t-tables as a substitute.

• Discrete Information: The Z-chart is primarily designed for steady information. Making use of it to discrete information can result in inaccuracies, particularly with small pattern sizes. In such circumstances, various strategies just like the binomial distribution could also be extra applicable.

• Interpolation: The Z-chart sometimes offers chances for particular Z-scores. To search out chances for Z-scores circuitously listed, interpolation is important, which might introduce slight inaccuracies.

Software program and Options

Whereas Z-charts are available, many statistical software program packages (e.g., R, SPSS, SAS, Python with SciPy) present extra exact and handy methods to calculate chances and Z-scores. These software program packages typically provide capabilities that instantly compute chances with out requiring guide lookup in a desk, eliminating potential errors related to interpolation. They’ll additionally deal with non-normal distributions by means of varied statistical methods.

Conclusion

The Z-chart, a seemingly easy desk, is a strong instrument for understanding and analyzing usually distributed information. Its purposes span various fields, from speculation testing and confidence intervals to high quality management and chance calculations. Nevertheless, it is essential to concentrate on its limitations, notably the idea of normality and the requirement of figuring out the inhabitants commonplace deviation. By understanding each the strengths and weaknesses of the Z-chart, you’ll be able to successfully leverage this important instrument in your statistical analyses, making certain correct and dependable conclusions. Bear in mind to at all times critically assess your information and select the suitable statistical technique primarily based on its traits and the analysis query at hand. When doubtful, consulting with a statistician can guarantee essentially the most sturdy and applicable evaluation is employed.

Closure

Thus, we hope this text has offered priceless insights into Decoding the Z-Chart: A Complete Information to Commonplace Regular Distribution. We thanks for taking the time to learn this text. See you in our subsequent article!