Decoding The Z-Rating Chart: A Complete Information To Understanding And Making use of Z-Scores In Statistics

Decoding the Z-Rating Chart: A Complete Information to Understanding and Making use of Z-Scores in Statistics

Associated Articles: Decoding the Z-Rating Chart: A Complete Information to Understanding and Making use of Z-Scores in Statistics

Introduction

On this auspicious event, we’re delighted to delve into the intriguing matter associated to Decoding the Z-Rating Chart: A Complete Information to Understanding and Making use of Z-Scores in Statistics. Let’s weave fascinating info and supply recent views to the readers.

Decoding the Z-Rating Chart: A Complete Information to Understanding and Making use of Z-Scores in Statistics

The Z-score, often known as the usual rating, is a basic idea in statistics used to measure what number of customary deviations a selected knowledge level lies above or beneath the imply of an information set. Its utility extends throughout quite a few fields, from high quality management and finance to schooling and healthcare, making the understanding and software of Z-scores essential for anybody working with quantitative knowledge. This text delves into the intricacies of Z-scores, exploring their calculation, interpretation, and software, with a selected give attention to the position of the Z-score chart (often known as a Z-table or customary regular desk).

Understanding Z-Scores: The Basis

A Z-score transforms uncooked knowledge factors from a traditional distribution into standardized values. This standardization permits for simple comparability of knowledge factors from completely different datasets with completely different means and customary deviations. The system for calculating a Z-score is:

Z = (X – μ) / σ

The place:

• Z represents the Z-score
• X represents the person knowledge level
• μ represents the inhabitants imply
• σ represents the inhabitants customary deviation

If the inhabitants parameters (μ and σ) are unknown, pattern statistics (x̄ and s) are used as estimates. Nonetheless, it is essential to keep in mind that utilizing pattern statistics introduces a component of uncertainty, notably with smaller pattern sizes.

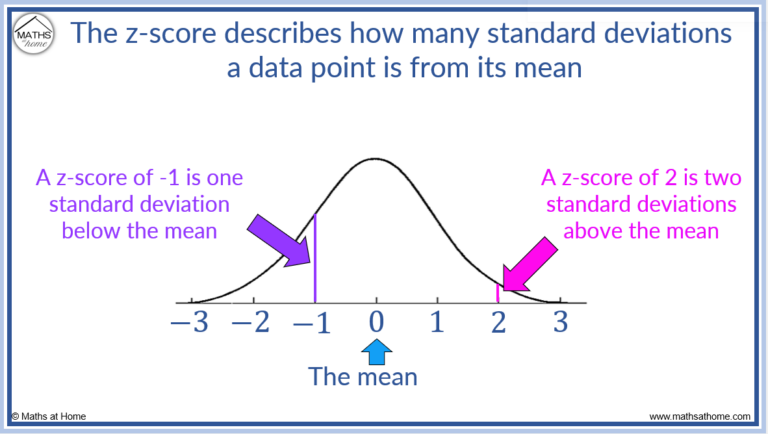
A optimistic Z-score signifies that the information level lies above the imply, whereas a destructive Z-score signifies that it lies beneath the imply. A Z-score of 0 signifies that the information level is strictly on the imply. The magnitude of the Z-score displays the space from the imply when it comes to customary deviations. As an example, a Z-score of 1.5 means the information level is 1.5 customary deviations above the imply.

The Significance of the Regular Distribution

The Z-score’s effectiveness depends closely on the idea of a traditional distribution. The conventional distribution, usually depicted as a bell curve, is characterised by its symmetry and particular properties. Many pure phenomena and datasets approximate a traditional distribution, making Z-scores a strong device in these contexts. Nonetheless, it is essential to evaluate the normality of the information earlier than making use of Z-scores. Checks just like the Shapiro-Wilk check or visible inspection of histograms and Q-Q plots can assist decide the normality of the information. If the information considerably deviates from normality, different strategies is perhaps extra acceptable.

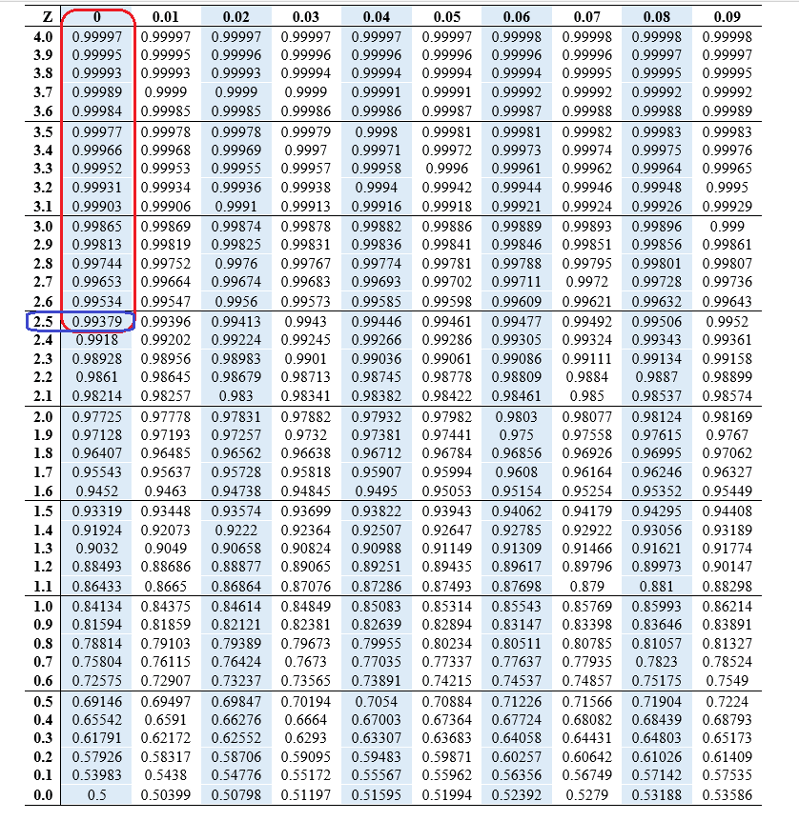
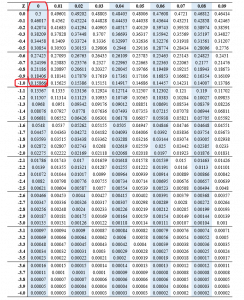
Introducing the Z-Rating Chart (Z-Desk)

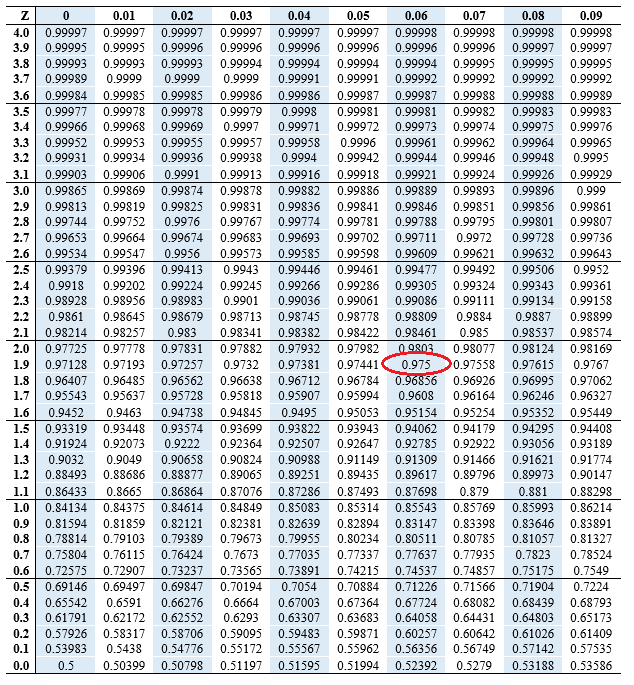
The Z-score chart, or Z-table, is an important device for decoding Z-scores. This desk supplies the cumulative chance (or space below the curve) to the left of a given Z-score in a normal regular distribution (imply = 0, customary deviation = 1). The desk usually lists Z-scores with their corresponding possibilities. As an example, a Z-score of 1.96 corresponds to a cumulative chance of roughly 0.975, that means there is a 97.5% probability of observing an information level lower than or equal to 1.96 customary deviations above the imply.

Utilizing the Z-Rating Chart: A Step-by-Step Information

1. Calculate the Z-score: Use the system talked about earlier to calculate the Z-score in your knowledge level.

2. Find the Z-score on the chart: The Z-table is often organized with Z-scores listed in rows and columns. Discover the row similar to the entire quantity and the primary decimal place of your Z-score. Then, discover the column similar to the second decimal place.

3. Discover the corresponding chance: The intersection of the row and column provides the cumulative chance (space to the left) of your Z-score.

4. Interpret the chance: This chance represents the proportion of knowledge factors within the distribution which are lower than or equal to your knowledge level. You should utilize this chance to find out varied statistics, together with percentiles, possibilities of exceeding a sure worth, and confidence intervals.

Purposes of Z-Scores and Z-Rating Charts

The functions of Z-scores and Z-score charts are huge and diverse:

• Figuring out Percentiles: Z-scores can be utilized to find out the percentile rank of an information level. For instance, a Z-score of 1.645 corresponds to the ninety fifth percentile, that means that 95% of the information factors lie beneath this worth.

• Speculation Testing: Z-scores are basic in speculation testing, notably when coping with giant pattern sizes. They’re used to calculate Z-statistics, that are then in comparison with vital values to find out whether or not to reject or fail to reject the null speculation.

• High quality Management: In manufacturing and high quality management, Z-scores are used to watch course of variation and determine outliers. Knowledge factors with excessive absolute Z-scores would possibly point out defects or course of points.

• Finance: Z-scores are utilized in monetary danger administration to evaluate the chance of default or chapter. The Altman Z-score, for example, is a extensively used creditworthiness indicator.

• Training: Z-scores are used to standardize check scores, permitting for comparability of scholar efficiency throughout completely different checks and years.

• Healthcare: Z-scores are utilized in varied medical functions, together with monitoring affected person important indicators and figuring out uncommon patterns which may point out well being issues.

Limitations of Z-Scores

Regardless of their vast applicability, Z-scores have limitations:

• Assumption of Normality: Z-scores are best when utilized to knowledge that follows a traditional distribution. Violation of this assumption can result in inaccurate interpretations.

• Sensitivity to Outliers: Outliers can considerably affect the imply and customary deviation, thereby affecting the calculated Z-scores. Sturdy statistical strategies is perhaps most well-liked when coping with important outliers.

• Interpretation Challenges with Non-Regular Knowledge: Whereas transformations can typically normalize knowledge, making use of Z-scores to severely non-normal knowledge can result in deceptive outcomes.

Conclusion

The Z-score chart, at the side of the Z-score calculation, supplies a strong device for understanding and decoding knowledge inside a statistical framework. Its capability to standardize knowledge and supply possibilities makes it indispensable throughout varied disciplines. Nonetheless, it is essential to recollect the assumptions underlying its use and to contemplate its limitations earlier than making use of it to any dataset. Cautious consideration of knowledge normality and potential outliers is important for correct and significant interpretation of Z-scores. By understanding each the strengths and limitations of Z-scores and the Z-score chart, researchers and practitioners can leverage this beneficial device successfully of their analyses.

Closure

Thus, we hope this text has supplied beneficial insights into Decoding the Z-Rating Chart: A Complete Information to Understanding and Making use of Z-Scores in Statistics. We recognize your consideration to our article. See you in our subsequent article!