Deep Dive Into The P-Chart UCL Formulation: Understanding And Making use of Management Charts For Proportion Information

Deep Dive into the p-Chart UCL Formulation: Understanding and Making use of Management Charts for Proportion Information

Associated Articles: Deep Dive into the p-Chart UCL Formulation: Understanding and Making use of Management Charts for Proportion Information

Introduction

With enthusiasm, let’s navigate by way of the intriguing subject associated to Deep Dive into the p-Chart UCL Formulation: Understanding and Making use of Management Charts for Proportion Information. Let’s weave fascinating data and supply recent views to the readers.

Deep Dive into the p-Chart UCL Formulation: Understanding and Making use of Management Charts for Proportion Information

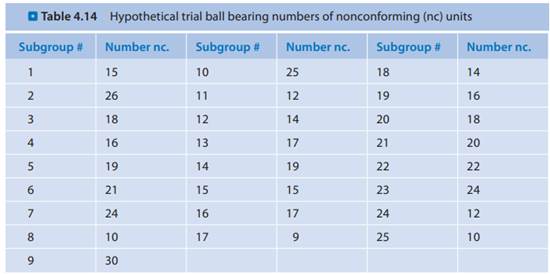
Management charts are important instruments in statistical course of management (SPC), offering a visible illustration of course of stability and serving to determine potential sources of variation. Among the many numerous management charts, the p-chart holds an important place for monitoring the proportion of nonconforming models in a course of. Understanding the components for its higher management restrict (UCL) is essential to successfully deciphering and using this highly effective device. This text will delve into the p-chart UCL components, exploring its derivation, sensible purposes, and issues for correct implementation.

Understanding the p-Chart and its Objective

A p-chart is designed to observe the proportion (p) of faulty or nonconforming gadgets in a pattern. In contrast to the x-bar chart which tracks the typical of a steady variable, the p-chart focuses on the proportion of a discrete attribute. As an example, a p-chart might monitor the proportion of faulty widgets produced on an meeting line, the proportion of buyer complaints obtained, or the speed of errors in an information entry course of.

The p-chart makes use of three management limits:

• Higher Management Restrict (UCL): The higher boundary past which a pattern proportion is taken into account statistically unlikely to happen if the method is in management.
• Middle Line (CL): The common proportion of nonconforming models over a time frame, representing the method common.
• Decrease Management Restrict (LCL): The decrease boundary beneath which a pattern proportion is taken into account statistically unlikely to happen if the method is in management.

The main target of this text is the UCL, because it’s typically probably the most important restrict in figuring out potential course of points. Factors plotted above the UCL sign a possible enhance within the proportion of nonconforming gadgets, prompting investigation and corrective actions.

Derivation of the p-Chart UCL Formulation

The UCL for a p-chart is derived from the ideas of statistical course of management and the binomial distribution. Assuming the proportion of nonconforming models follows a binomial distribution, the components for the UCL is:

UCL = p̄ + 3√(p̄(1-p̄)/n)

The place:

• UCL: The higher management restrict.
• p̄ (p-bar): The common proportion of nonconforming models throughout all samples. That is calculated by summing the proportions of nonconforming models in every pattern and dividing by the variety of samples.
• n: The pattern dimension (variety of models inspected in every pattern). It is essential that the pattern dimension stays constant throughout all samples for correct interpretation.

Let’s break down the components’s parts:

• p̄: This represents the central tendency of the method, indicating the typical proportion of defects. A secure and well-controlled course of may have a comparatively constant p̄ worth.

• p̄(1-p̄): This time period represents the variance of the binomial distribution. It is maximized when p̄ = 0.5, indicating the best uncertainty within the proportion. As p̄ approaches 0 or 1, the variance decreases, reflecting larger certainty within the proportion.

• /n: Dividing by the pattern dimension (n) reduces the variance. Bigger pattern sizes result in extra exact estimates of the proportion and narrower management limits. It is because bigger samples present extra details about the method, resulting in a extra dependable estimate of the true proportion of nonconforming models.

• 3√(…): This time period represents three normal deviations (3σ) of the sampling distribution. Using three normal deviations is a conference based mostly on the empirical rule, which states that roughly 99.7% of the info in a standard distribution falls inside three normal deviations of the imply. This ensures a excessive degree of confidence that factors outdoors the management limits signify a real shift within the course of fairly than random variation.

Sensible Purposes and Issues

The p-chart finds widespread software in numerous industries, together with manufacturing, healthcare, and repair sectors. Some examples embody:

• Manufacturing: Monitoring the proportion of faulty merchandise in a manufacturing line.
• Healthcare: Monitoring the an infection fee in a hospital.
• Buyer Service: Measuring the proportion of buyer complaints resolved inside a selected timeframe.
• Software program Improvement: Monitoring the bug fee in software program releases.

Nonetheless, a number of essential issues should be addressed for correct and efficient software of the p-chart:

• Pattern Measurement Consistency: Sustaining a constant pattern dimension (n) throughout all samples is paramount. Variations in pattern dimension will distort the variance calculation and result in inaccurate management limits.

• Independence of Samples: Samples needs to be impartial of one another. If samples are taken sequentially and the method is very autocorrelated, the belief of independence is violated, resulting in inaccurate management limits.

• Rational Subgrouping: Samples needs to be rationally subgrouped to seize the inherent variability within the course of. For instance, samples taken from totally different machines or totally different shifts would possibly reveal totally different patterns of variation.

• Enough Information: A adequate variety of samples (sometimes at the very least 20-25) is required to precisely estimate p̄ and guarantee dependable management limits. Inadequate knowledge can result in inaccurate estimates and unreliable management limits.

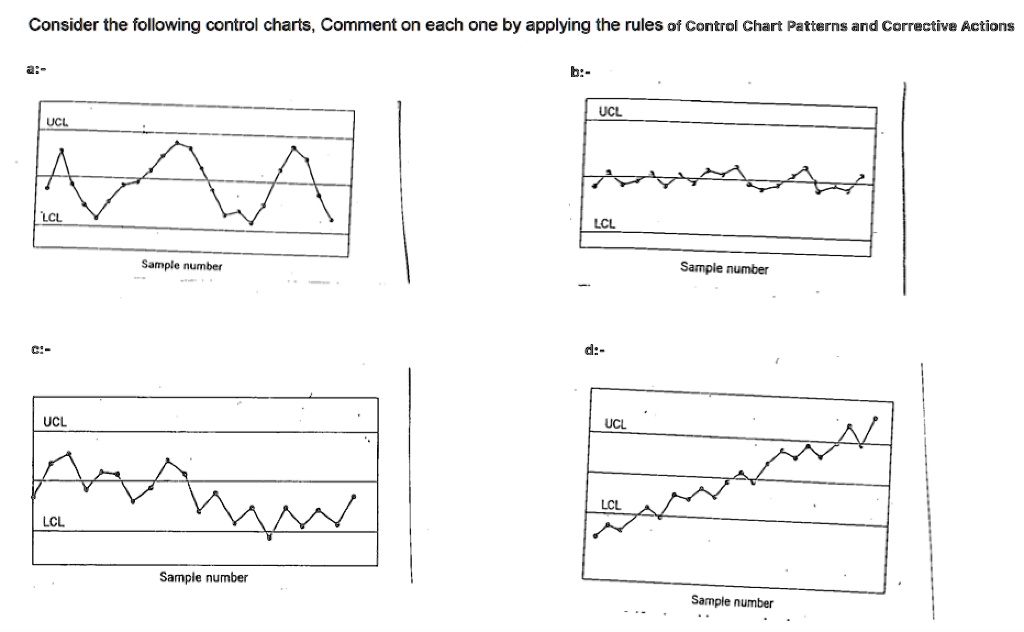
• Course of Stability: The p-chart assumes that the method is secure (in management) when the management limits are established. If the method will not be secure, the management limits might be inaccurate, and the chart won’t present a dependable illustration of course of efficiency.

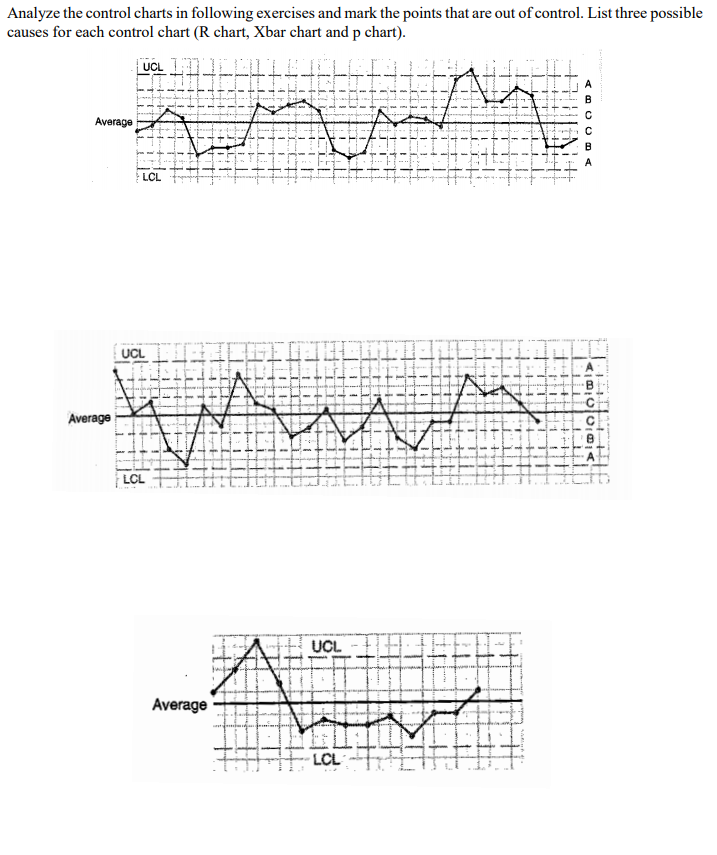
• Out-of-Management Factors: Factors plotted outdoors the management limits point out potential course of instability. Investigating the causes of out-of-control factors is essential to determine and proper issues, stopping additional manufacturing of nonconforming models.

• Decrease Management Restrict (LCL): In some instances, the calculated LCL could be adverse. Since a proportion can’t be adverse, the LCL is usually set to zero in such conditions.

Software program and Instruments for p-Chart Building

A number of statistical software program packages and on-line instruments facilitate the development and evaluation of p-charts. These instruments automate the calculations, plotting, and interpretation of the chart, saving effort and time. Some common choices embody:

• Minitab: A extensively used statistical software program bundle with complete SPC capabilities.
• JMP: One other highly effective statistical software program bundle providing superior options for knowledge evaluation and visualization.
• Microsoft Excel: Whereas not as specialised as devoted SPC software program, Excel can be utilized to create primary p-charts with the assistance of add-ins or customized formulation.
• On-line Calculators: A number of on-line calculators can be found that permit customers to enter knowledge and robotically generate p-charts with their respective UCL, CL, and LCL.

Conclusion

The p-chart, with its UCL components on the core, is a precious device for monitoring and controlling the proportion of nonconforming models in a course of. By understanding the components’s derivation and contemplating the sensible purposes and limitations, practitioners can successfully leverage the p-chart to enhance course of efficiency, cut back defects, and improve general high quality. Correct interpretation and well timed response to out-of-control alerts are important for maximizing the advantages of this highly effective SPC device. Remembering the significance of constant pattern sizes, rational subgrouping, and adequate knowledge is essential for making certain the reliability and accuracy of the p-chart evaluation. Lastly, using acceptable software program or instruments can considerably streamline the method of making and deciphering p-charts, enabling environment friendly course of monitoring and enchancment.

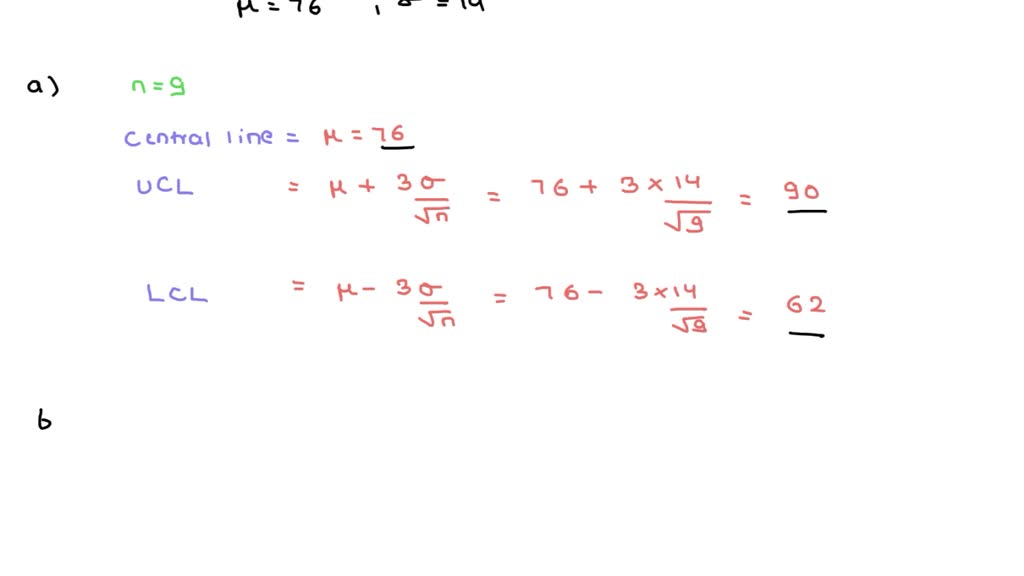
Closure

Thus, we hope this text has supplied precious insights into Deep Dive into the p-Chart UCL Formulation: Understanding and Making use of Management Charts for Proportion Information. We hope you discover this text informative and helpful. See you in our subsequent article!