Understanding And Making use of The Higher Management Restrict Components In Management Charts

Understanding and Making use of the Higher Management Restrict Components in Management Charts

Associated Articles: Understanding and Making use of the Higher Management Restrict Components in Management Charts

Introduction

With enthusiasm, let’s navigate by way of the intriguing subject associated to Understanding and Making use of the Higher Management Restrict Components in Management Charts. Let’s weave attention-grabbing info and provide contemporary views to the readers.

Understanding and Making use of the Higher Management Restrict Components in Management Charts

Management charts are highly effective statistical instruments utilized in high quality management and course of enchancment to watch the soundness and efficiency of a course of over time. They visually show information factors plotted towards management limits, offering a transparent indication of whether or not a course of is in management (steady and predictable) or uncontrolled (unstable and doubtlessly producing faulty outputs). A vital component of any management chart is the higher management restrict (UCL), which represents the higher boundary past which a course of is deemed statistically unlikely to function if it is actually in management. Understanding the UCL method and its utility is significant for efficient course of monitoring and enchancment.

This text delves into the varied formulation used to calculate the UCL for several types of management charts, exploring their underlying assumptions, sensible functions, and limitations. We are going to cowl the commonest management charts, together with X-bar and R charts, X-bar and s charts, p-charts, c-charts, and u-charts, offering a complete information to understanding and using the UCL for every.

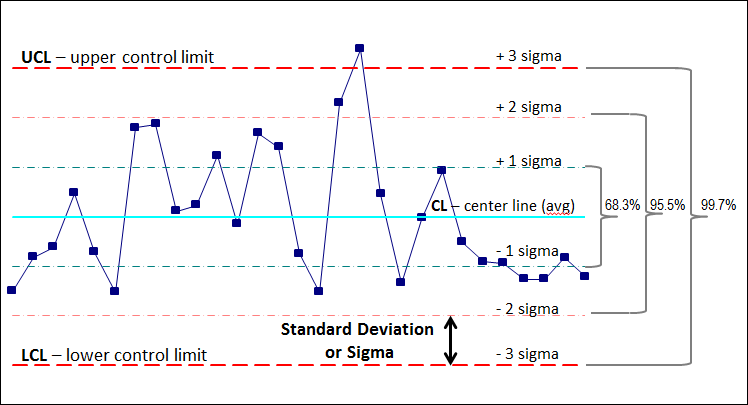
1. The Fundamentals of Management Charts and Management Limits

Management charts are based mostly on the ideas of statistical course of management (SPC). They make the most of pattern information collected over time to estimate the method imply and variability. These estimates are then used to calculate the management limits, which signify the anticipated vary of variation for a course of working in a state of statistical management. The management limits are usually not arbitrary; they’re statistically decided based mostly on the method information and the chosen confidence stage (sometimes 99.73%, corresponding to 3 commonplace deviations from the imply in a traditional distribution).

A typical management chart consists of:

• Central Line: Represents the typical (imply) of the method information.
• Higher Management Restrict (UCL): The higher boundary past which a knowledge level suggests the method is uncontrolled.
• Decrease Management Restrict (LCL): The decrease boundary under which a knowledge level suggests the method is uncontrolled.

Factors falling exterior the management limits sign potential issues throughout the course of, prompting investigation and corrective actions. Factors constantly clustering close to the management limits may also point out potential points, even when they continue to be throughout the limits.

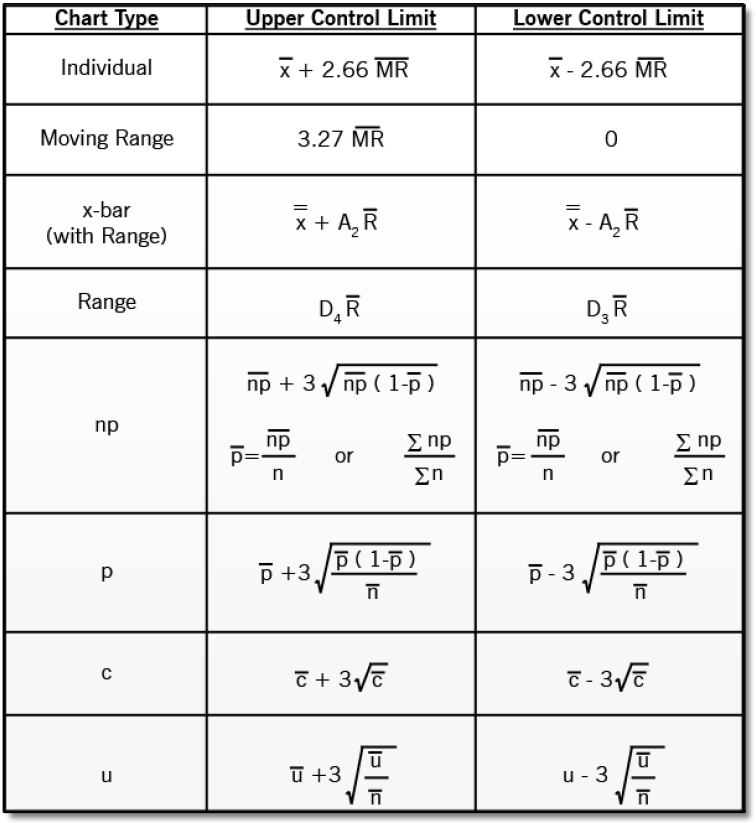
2. UCL Formulation for Totally different Management Charts

The UCL method varies relying on the kind of information being monitored and the particular management chart used. This is a breakdown of probably the most generally used management charts and their respective UCL formulation:

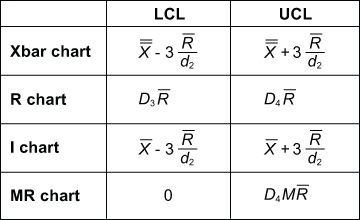
2.1. X-bar and R Charts (Variable Knowledge):

X-bar and R charts are used to watch the typical (X-bar) and vary (R) of a steady variable. They’re appropriate for monitoring processes the place the info is measured on a steady scale (e.g., weight, size, temperature).

• X-bar Chart: The UCL for the X-bar chart is calculated as:

  UCL = X-double bar + A2 * R-bar

  The place:

  • X-double bar is the typical of the pattern means.
  • R-bar is the typical of the pattern ranges.
  • A2 is a management chart fixed that relies on the pattern dimension (n). These constants are available in statistical tables.

• R Chart: The UCL for the R chart is calculated as:

  UCL = D4 * R-bar

  The place:

  • R-bar is the typical of the pattern ranges.
  • D4 is a management chart fixed that relies on the pattern dimension (n). These constants are additionally present in statistical tables.

2.2. X-bar and s Charts (Variable Knowledge):

X-bar and s charts are an alternative choice to X-bar and R charts, significantly helpful when the pattern dimension is bigger (usually n > 10). They use the pattern commonplace deviation (s) as an alternative of the vary (R) to estimate course of variability.

• X-bar Chart: The UCL for the X-bar chart is calculated as:

  UCL = X-double bar + A3 * s-bar

  The place:

  • X-double bar is the typical of the pattern means.
  • s-bar is the typical of the pattern commonplace deviations.
  • A3 is a management chart fixed that relies on the pattern dimension (n).

• s Chart: The UCL for the s chart is calculated as:

  UCL = B4 * s-bar

  The place:

  • s-bar is the typical of the pattern commonplace deviations.
  • B4 is a management chart fixed that relies on the pattern dimension (n).

2.3. p-Charts (Attribute Knowledge):

p-charts are used to watch the proportion of nonconforming models in a pattern. They’re appropriate for attribute information the place every unit is assessed as both conforming or nonconforming (e.g., faulty or non-defective).

The UCL for a p-chart is calculated as:

UCL = p-bar + 3 * sqrt(p-bar * (1 - p-bar) / n)

The place:

• p-bar is the typical proportion of nonconforming models throughout all samples.
• n is the pattern dimension.

2.4. c-Charts (Attribute Knowledge):

c-charts are used to watch the variety of nonconformities (defects) per unit. They’re appropriate for conditions the place the variety of defects is counted in a hard and fast unit of measurement (e.g., the variety of scratches on a painted floor).

The UCL for a c-chart is calculated as:

UCL = c-bar + 3 * sqrt(c-bar)

The place:

• c-bar is the typical variety of nonconformities per unit throughout all samples.

2.5. u-Charts (Attribute Knowledge):

u-charts are much like c-charts however are used when the pattern dimension varies from pattern to pattern. They monitor the variety of nonconformities per unit, however the unit dimension is just not fixed.

The UCL for a u-chart is calculated as:

UCL = u-bar + 3 * sqrt(u-bar / n)

The place:

• u-bar is the typical variety of nonconformities per unit throughout all samples.
• n is the pattern dimension (which may fluctuate between samples).

3. Assumptions and Limitations

The formulation offered above depend on a number of assumptions, together with:

• Knowledge Independence: Knowledge factors ought to be impartial of one another; that’s, the result of 1 pattern mustn’t affect the result of one other.
• Knowledge Normality: Whereas some management charts are sturdy to departures from normality, particularly for bigger pattern sizes, the underlying calculations assume that the info follows a traditional distribution.
• Course of Stability: The management limits are calculated based mostly on the idea that the method is steady (in management) throughout the preliminary information assortment interval. If the method is just not steady throughout this era, the calculated management limits will probably be inaccurate.
• Fixed Variability: For X-bar and R/s charts, the idea is made that the method variability stays comparatively fixed over time.

Violations of those assumptions can result in inaccurate management limits and deceptive interpretations of the chart. It is essential to fastidiously look at the info and assess the validity of those assumptions earlier than implementing and decoding management charts.

4. Sensible Purposes and Interpretations

Management charts are extensively used throughout varied industries, together with manufacturing, healthcare, and repair sectors, for monitoring and bettering course of efficiency. Their functions embrace:

• Early Detection of Course of Shifts: Management charts present early warning alerts of adjustments within the course of imply or variability, permitting for well timed intervention and prevention of defects.
• Course of Functionality Evaluation: Management charts can be utilized along with course of functionality research to evaluate whether or not a course of is able to assembly specified high quality necessities.
• Root Trigger Evaluation: When some extent falls exterior the management limits, the management chart serves as a place to begin for investigating the basis causes of the variation and implementing corrective actions.
• Steady Enchancment: Management charts facilitate steady enchancment efforts by offering a visible illustration of course of efficiency over time and enabling the monitoring of enchancment initiatives.

5. Software program and Instruments

Numerous statistical software program packages (e.g., Minitab, JMP, R) and spreadsheet applications (e.g., Microsoft Excel) provide built-in functionalities for creating and analyzing management charts. These instruments automate the calculation of management limits and supply varied diagnostic options for decoding the charts.

Conclusion:

The higher management restrict is a basic element of management charts, offering a essential threshold for figuring out potential course of instability. Understanding the varied UCL formulation for various management chart sorts is crucial for efficient course of monitoring and enchancment. Whereas the formulation present a mathematical foundation for figuring out the UCL, it is essential to recollect the underlying assumptions and limitations of management charts and to interpret the outcomes throughout the context of the particular course of being monitored. By fastidiously making use of these ideas and using applicable software program instruments, management charts could be a highly effective device for enhancing high quality and effectivity in any group.

Closure

Thus, we hope this text has offered helpful insights into Understanding and Making use of the Higher Management Restrict Components in Management Charts. We respect your consideration to our article. See you in our subsequent article!