Understanding The Space To The Left Of A Z-Rating: A Complete Information

Understanding the Space to the Left of a Z-Rating: A Complete Information

Associated Articles: Understanding the Space to the Left of a Z-Rating: A Complete Information

Introduction

With nice pleasure, we’ll discover the intriguing matter associated to Understanding the Space to the Left of a Z-Rating: A Complete Information. Let’s weave fascinating data and supply recent views to the readers.

Understanding the Space to the Left of a Z-Rating: A Complete Information

The usual regular distribution, usually represented by the Z-distribution, is a cornerstone of statistical evaluation. Its bell-shaped curve, completely symmetrical round a imply of 0 and an ordinary deviation of 1, gives a framework for understanding and deciphering chance distributions of varied knowledge units. A vital side of working with the Z-distribution includes understanding the realm to the left of a selected Z-score. This space represents the cumulative chance of observing a worth lower than or equal to that Z-score. This text will delve deeply into the idea, its purposes, and its implications in statistical inference.

The Z-Rating and its Significance:

A Z-score, also referred to as an ordinary rating, signifies what number of customary deviations a selected knowledge level is away from the imply of its distribution. A optimistic Z-score signifies that the information level lies above the imply, whereas a unfavourable Z-score signifies it lies beneath the imply. The method for calculating a Z-score is:

Z = (X – μ) / σ

The place:

• Z is the Z-score
• X is the person knowledge level
• μ is the inhabitants imply
• σ is the inhabitants customary deviation

The transformation of uncooked knowledge into Z-scores permits us to check knowledge factors from completely different distributions with various means and customary deviations. This standardization simplifies statistical evaluation and facilitates the usage of the usual regular distribution desk (also referred to as the Z-table).

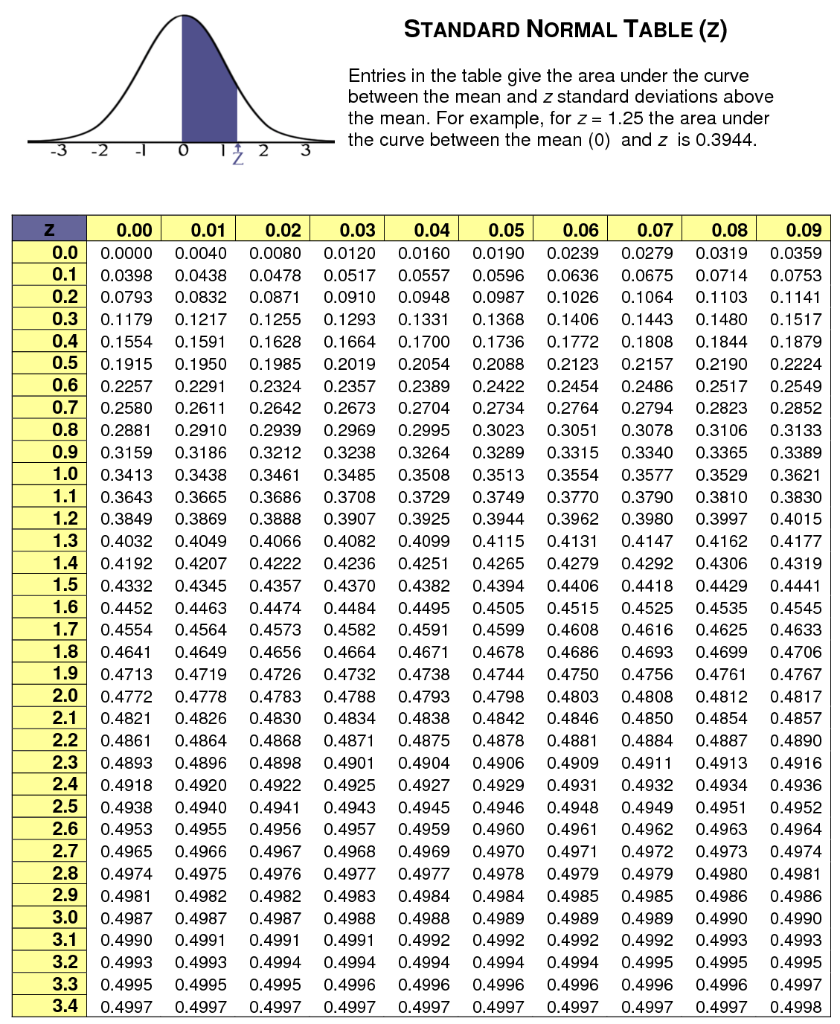
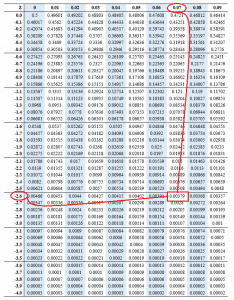
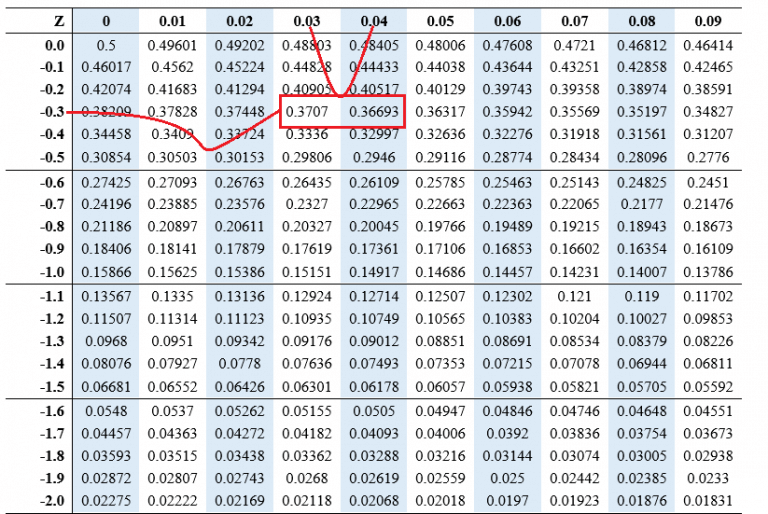
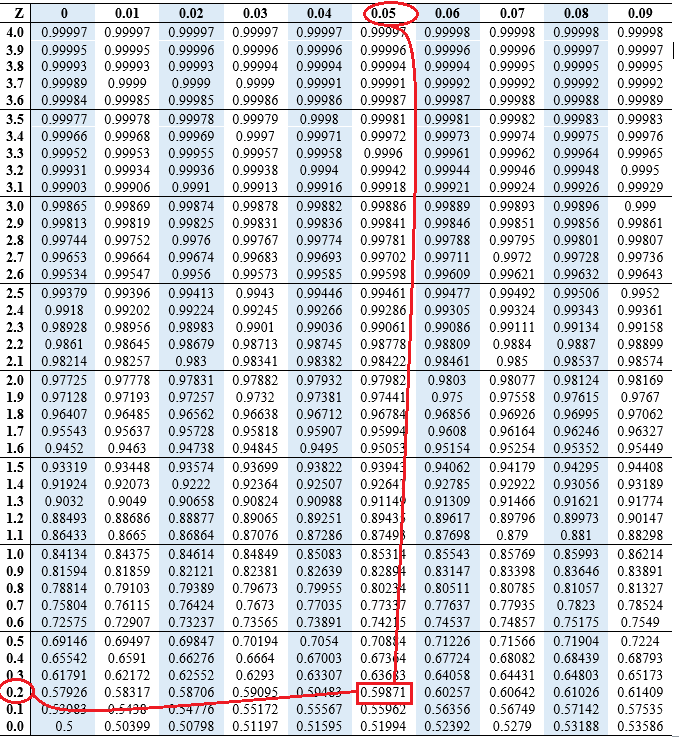
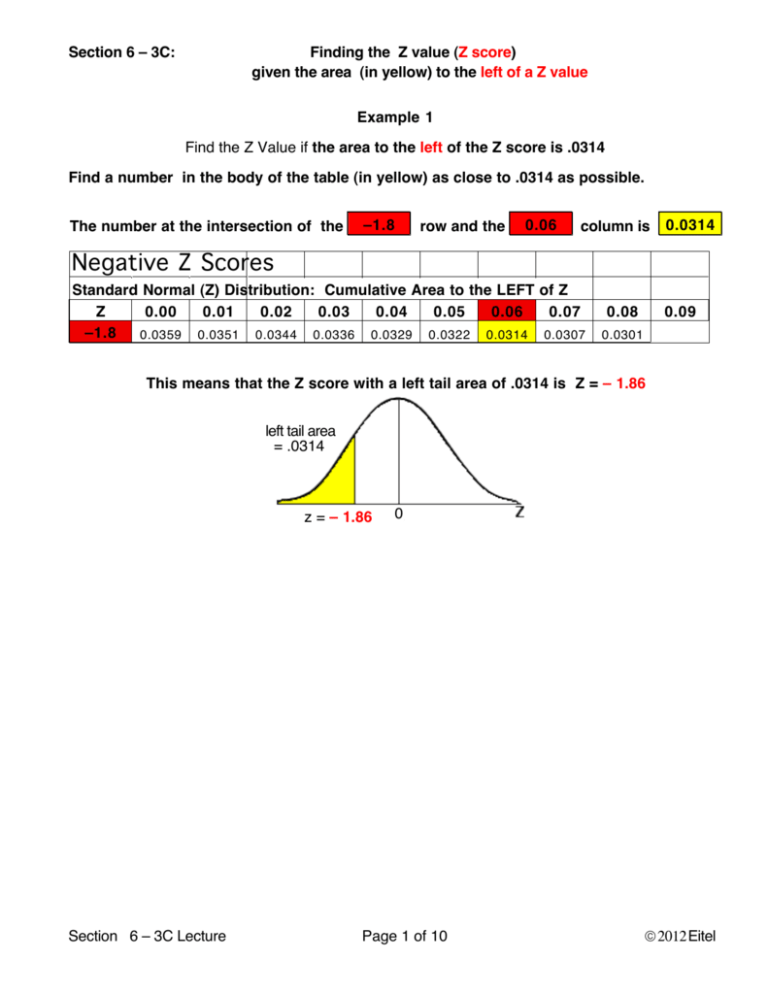
The Z-Desk and Cumulative Chance:

The Z-table is an important software for figuring out the realm to the left of a selected Z-score. This desk gives the cumulative chance, which represents the chance of observing a worth lower than or equal to a given Z-score. The desk is often organized with Z-scores listed to 2 decimal locations, with the primary decimal place represented within the rows and the second decimal place within the columns. The intersection of a row and column gives the corresponding cumulative chance.

For instance, if we need to discover the realm to the left of Z = 1.50, we’d find 1.5 within the row and 0.00 within the column. The intersecting worth within the desk would symbolize the cumulative chance, which is roughly 0.9332. This implies that there’s a 93.32% chance of observing a worth lower than or equal to 1.5 customary deviations above the imply in an ordinary regular distribution.

Decoding the Space to the Left:

The realm to the left of a Z-score has a number of vital interpretations:

• Chance: It represents the chance of a randomly chosen knowledge level falling beneath the desired Z-score.
• Percentile Rank: It signifies the percentile rank of the information level. As an example, a Z-score with an space of 0.80 to its left corresponds to the eightieth percentile. Which means 80% of the information factors within the distribution fall beneath this worth.
• Proportion: It displays the proportion of information factors within the distribution which might be lower than or equal to the Z-score.

Purposes of the Space to the Left:

The idea of the realm to the left of a Z-score finds in depth purposes throughout numerous fields:

• Speculation Testing: In speculation testing, the realm to the left of a Z-score (or its complement, the realm to the best) is used to find out the p-value, which helps in deciding whether or not to reject or fail to reject the null speculation. That is significantly essential in figuring out statistical significance.

• Confidence Intervals: When establishing confidence intervals, the Z-score akin to a desired confidence degree (e.g., 95%) is used. The realm to the left of this Z-score helps decide the margin of error and the interval’s boundaries.

• High quality Management: In high quality management processes, Z-scores and their corresponding areas are used to observe course of variability and determine outliers. This helps make sure that services or products meet specified high quality requirements.

• Finance and Funding: Z-scores are employed in monetary modeling to evaluate danger and analyze funding efficiency. The realm to the left of a selected Z-score might help decide the chance of experiencing a selected degree of return or loss.

• Medication and Healthcare: In medical analysis and medical trials, Z-scores and their related chances are used to research the effectiveness of remedies and to evaluate the importance of medical outcomes.

Limitations and Concerns:

Whereas the Z-table and the realm to the left of a Z-score are highly effective instruments, it is essential to acknowledge their limitations:

• Assumption of Normality: The Z-table is predicated on the belief that the information follows a standard distribution. If the information is considerably non-normal, utilizing the Z-table might result in inaccurate outcomes. In such instances, non-parametric strategies could also be extra applicable.

• Pattern Dimension: The accuracy of the Z-score and its related space improves with bigger pattern sizes. With small pattern sizes, the approximation supplied by the Z-table is probably not as dependable.

• Inhabitants Parameters: The calculation of Z-scores requires information of the inhabitants imply and customary deviation. If these parameters are unknown, they have to be estimated from pattern knowledge, which introduces some uncertainty.

• Discrete vs. Steady Information: The Z-table is designed for steady knowledge. When coping with discrete knowledge, changes could also be needed to enhance the accuracy of the chance calculations.

Technological Developments:

The appearance of statistical software program packages and on-line calculators has considerably simplified the method of figuring out the realm to the left of a Z-score. These instruments usually present extra exact calculations than conventional Z-tables and may deal with extra advanced eventualities. They remove the necessity for guide interpolation and scale back the danger of human error.

Conclusion:

The realm to the left of a Z-score is a basic idea in statistical evaluation with far-reaching purposes. Understanding its interpretation and its use in numerous statistical procedures is crucial for anybody working with knowledge. Whereas the Z-table gives a handy software for calculating chances, it is essential to contemplate the assumptions and limitations related to its use. The mix of theoretical understanding and the utilization of recent statistical instruments ensures correct and dependable evaluation of information, resulting in knowledgeable choices and sturdy conclusions. The mastery of this idea empowers analysts to successfully interpret chance distributions, make inferences about populations, and draw significant conclusions from knowledge throughout various fields.

Closure

Thus, we hope this text has supplied helpful insights into Understanding the Space to the Left of a Z-Rating: A Complete Information. We hope you discover this text informative and useful. See you in our subsequent article!